Math and science both use numbers in their respective field, but how do you think they differ? Here is a quick reference chart at what is covered more in-depth further along.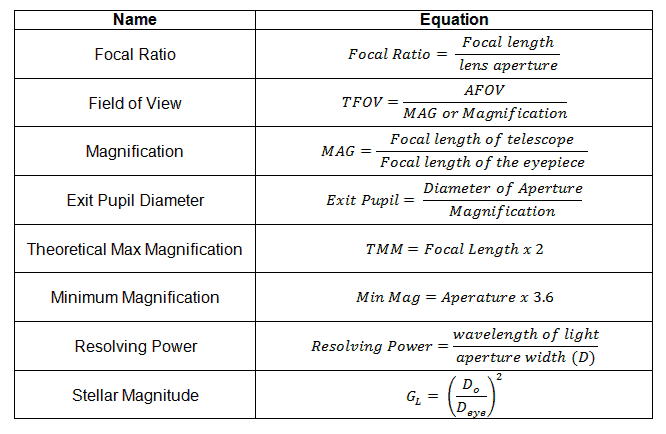
In Math, numbers are mere figures manipulated and computed to produce another number. In contrast, Science associate numbers with a reference which result in what we call “units of measurement”.
If we recall, Astronomy is the science that studies stars, planets, and other celestial bodies that makes up the universe. This field is not just about staring into the dark skies but rather a scientific method of observing those heavenly bodies.
In studying Astronomy, we have to educate ourselves with the common formulas used in this field. To know these formulas, we have gone over the main formulas needed in a simple discussion with examples for more natural understanding. So, people like me can get it.
Download our FREE equation calculator sheet. It shows some common popular brands and you can put your telescope in to find out all of the equations talked about here. Click here to get to the download.
Focal Ratio
The focal ratio or f/stop is considered as the “speed” of the optics in any telescope or device which uses a lens mechanism. This measurement is computed by dividing the focal length by the lens’ aperture.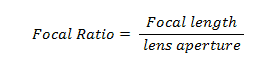
Sample Computation: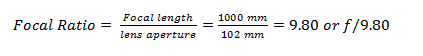
You have a telescope whose lens aperture is 102 millimeters and focal length of 1000 millimeters.
When solving for the focal ratio, make sure the units of the focal length and aperture are the same so that they will cancel out.
After that, perhaps, your next question would be, which should I prioritize when choosing a telescope? Is it the aperture or the focal length?
If you plan to go for deep space observation, then aperture must be your priority of choosing. However, if it is just space objects in the solar system, the aperture will not be that important.
The next thing you need to consider is the size of the celestial body you aim to observe. For smaller bodies, you need to have a longer focal length and high magnification telescope. Whereas, for larger bodies, you need to have a telescope with shorter aperture and low magnification rating.
A telescope with a focal length of 400 mm will enable you to observe objects such as large clusters of stars, the core of Andromeda galaxy, lunar phenomena (low magnifications) and the Orion nebula.
Meanwhile, a 900 mm telescope will enable you to observe planets in the solar system (Jupiter, Mars, Saturn, and Venus) lunar phenomena (high magnifications) and M57 the Ring-Shaped Nebula.
If you were looking at the aperture specs of a telescope, a 60 mm and 70 mm aperture would be too small for it. The telescope’s aperture affects two factors:
- Amount of Light: A telescope with a larger aperture is more able to capture huge amounts of light from the object.
- High Resolution: To have a feasible computation for the maximum resolution of a telescope, you multiply the lens aperture in millimeters by two. Example: 60 mm times two is equal to 120x magnifying power.
A telescope with focal length 400 mm and aperture 10 mm has a magnification of: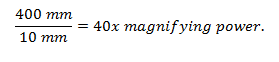
Field of View
Field of View (FOV) refers to the amount of space in the sky which you can see in the telescope’s eyepiece. This measurement is either expressed in degrees or a fraction thereof.
When observing through the eyepiece, the amount of space in the sky you see is the True Field of View (TFOV). Understanding this is essential so that you can compare the things you see in the eyepiece with the printed star charts produced by computers.
For instance, two stars separated by one-degree can be viewed at the same time when using a combination of telescope and eyepiece which provides a TFOV of one-degree or higher.
In calculating for the TFOV, you need to grab the measurement of the telescope’s focal length, eyepiece, and the apparent field of view (AFOV). No worries, as these three variables are often specified in the telescope already. Nevertheless, the general AFOV for the majority of Plossl eyepieces is 50 degrees.
Below are the formulas used to compute for the TFOV:
Sample Computation:
For instance, you have a telescope with a focal length of 1200 mm and an eyepiece with a focal length 25 mm. The AFOV specified in the Plossl eyepiece of the scope is 50 degrees. Compute for the TFOV of the scope.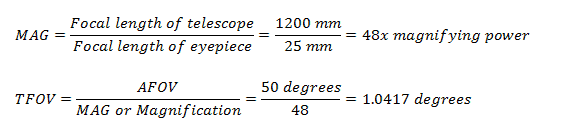
Based on the computations, the true field of view for that specified scope is 1.0417 degrees. You can also express this answer in arcminutes by multiplying 1.0417 by 60 equals 62.50 arcminutes or 62.50’.
What Are Some Setbacks From This Method?
- The eyepiece is a spherical surface, and calculating the TFOV assumes it is a plane surface. Consequently, the translation of AFOV to TFOV is not that accurate and expected to have some distortions even if the AFOV is accurately given.
- It is a typical case where the specified AFOV in scope would differ around +, or – 5 degrees.
- The specified and actual focal lengths of the telescope and the aperture differ by around 5 percent. This slight variation can affect the real true field of view perceived by the observer.
Despite these setbacks, still, this computation provides a good estimation for the actual field of view for any scope. It is a practical and straightforward method.
Magnification
The magnification or power of any telescope is its capacity to enlarge the size of objects. Comparing, magnification, and field of view, the latter is most important when choosing a scope.
Computing for the magnification of a telescope is direct and straightforward. Below is its formula.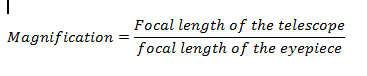
Sample Computation:
For instance, you have a telescope with a focal length of 1000 mm and an eyepiece with a focal length 20 mm. Compute for its magnification.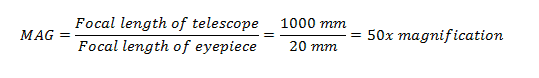
Exit Pupil Diameter
Exit pupil diameter is frequently confused with magnification, but it shouldn’t be because of the difference in their concept. This refers to the size of the light cone which exits from the eyepiece and enters the observer’s eye.
The formula for Exit Pupil Diameter: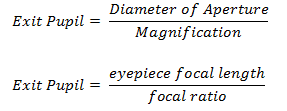
Sample Computation:
For instance, you have a telescope with an aperture focal length of 100 mm, eyepiece focal length 10 mm, scope focal length 500 mm, and magnification power of 50x. Compute for the exit pupil diameter of the scope.
Theoretical Maximum Magnification
The theoretical maximum magnification of a telescope refers to the ceiling limit of its power to enlarge objects. This can be computed by multiplying the scope’s aperture in inches by 50 or aperture focal length in millimeters times two.
Consequently, a 3-inch scope has a theoretical maximum magnification of 150x, whereas a 5-inch scope has 250x theoretical maximum magnification power.
Sample Computation:
For instance, you have a telescope with an aperture diameter of 100 mm. Compute for its theoretical maximum magnification.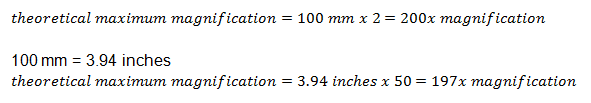
Why Can’t We Magnify Objects As Large As It Needs To Be?
There are two main reasons why this is not possible.
- The telescope itself limits the amount of light coming into the eyepiece and its magnification.
- The telescope itself limits the accurate resolution of the object’s details as it is being enlarged tremendously.
- The Earth’s atmosphere is one major factor affecting the accurateness of your viewing. If the atmosphere is turbulent, then you would experience a hard time seeing a clear image of the object.
Minimum Magnification
If there is a theoretical maximum magnification, its counterpart is the minimum magnification. This feature is based on the exit pupil diameter of the telescope.
Exit pupil diameter is the size of light which exits the eyepiece and enters the observer’s eye. To have a brighter more vivid image, the exit pupil diameter should be larger. Anything over 7mm is wasted due to the human eye can not accept more light than the diameter of a dilated pupil.
If there is a rule of thumb for theoretical maximum magnification, there is as well for minimum magnification. The rule of thumb for minimum magnification, a focal length of aperture in inches multiplied by 3.6 or aperture in millimeters divided by 7.
Sample Computation:
You have a telescope with an aperture focal length of 4 inches or 101.6 mm. Compute for its minimum magnification.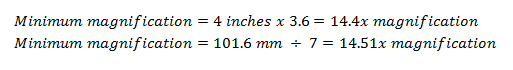
Resolving Power
Resolving power of a telescope or any optical instrument is its ability to measure the slightest distance between two objects which can be observed as two separate things.
A telescope with high resolving power can allow you to clearly see the smallest minimum distance between two objects that are close to each other.
Below is the formula for calculating the resolving power of a telescope: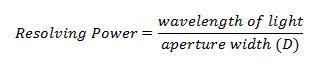
Sample Computation:
For instance, the aperture width of your telescope is 300 mm, and you are observing a yellow light having a wavelength of 590 nm or 0.00059 mm. Compute for the resolving power of the scope.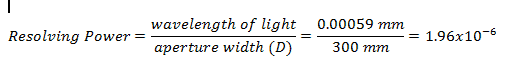
Stellar Magnitude Limit
The Stellar Magnitude Limit of the scope refers to its ability to allow the observer to see the faintest star in the sky.
Hundreds of years ago, the brightness of a star is expressed in “magnitudes” by Astronomers. This system was invented by the Greeks, where the brightest star is the first magnitude while the star with the weakest light is the sixth magnitude.
This method of measurement was very vague and broad, but when telescopes and other scientific inventions came, the accurate measures were slowly established.
Light grasp (GL) is the term for the amount of light a telescope can collect in its optical system.
The formula for the GL is: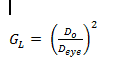
Where:
GL= light grasp
DO= diameter of the objective
Deye= diameter of the eye pupil
Meanwhile, the formula for the Stellar Magnitude Limit is: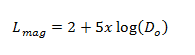
Sample Computation:
You want to observe a particular star with a magnitude of 8.8 using your current telescope with an objective diameter of 100 mm. Do you think your telescope is capable of viewing this star?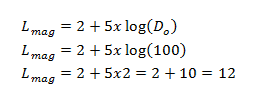
Based on the computation, the magnitude of the faintest star your scope is capable of viewing is 12. Consequently, the star with magnitude 8.8 can be viewed using your current telescope.
Need More?
Stargazing or observing the heavenly bodies can be an enjoyable and fun learning experience. To fully understand and appreciate this field though, you do need to have certain math skills (sorry), which are relevant to properly selecting the telescope which will better suit your needs.
Likewise, this field definitely sharpens your mind and imagination as you explore things out there. If you liked this article, you might like these two articles, “What is a Refractor, or What is a Reflector Telescope.” Astronomy and telescopes are scientific “things,” and you just can’t do science without math.
Will Montgomery explains core astronomy formulas with examples — using his technical background to make complex math easy for beginners and hobbyists.


